Liceu de Camocim Deputado Murilo Aguiar.
Disciplina: Matemática
Professor (a): Nayara
Série: 3ºE Turno: Tarde
Entrega: 23/06/2009
Ginga de Matemática
(Grupo de Circunferência)
Camocim-ce
Junho-2009
Alunos responsáveis pela Peça Teatral
Ana Técia
Nº. 01
Antônio Carvalho
Nº. 03
Dayane Portela
Nº. 13
Kervely
Nº. 31
Leydiane
Nº. 33
Alunos responsáveis pela resolução das questões do livro
Keyliane
Nº. 32
Luíza
Nº. 38
Leydiane
Nº. 33
Niele
Nº. 41
Rafael
Nº. 43
Alunos responsáveis pela confecção do livro
Antônio Carvalho
Keyliane
Niele
Alunos responsáveis Pelo BLOG
Keyliane
Nº. 32
Nayane
Nº. 40
Niele
Nº. 41
Rafael
Nº. 43
Alunos responsáveis pelas fotos do BLOG
Ana Técia
Nº. 01
Kervely
Nº. 31
Rafael
Nº. 43
Quem compareceu as reuniões do grupo
01
Ana Técia
Nº. 01
P
02
Carvalho
Nº. 03
P
03
Dayane Monteiro
Nº. 11
P
04
Dayane Portela
Nº. 13
P
05
Edvânia
Nº. 15
F
06
Janielly
Nº. 23
P
07
Janilly
Nº. 24
P
08
Kervely
Nº. 31
P
09
Keyliane
Nº. 32
P
10
Leydiane
Nº. 33
P
11
Luíza
Nº. 38
F
12
Nayane
Nº. 40
P
13
Niele
Nº. 41
P
14
Nilzilândia
Nº. 42
F
15
Rafael
Nº. 43
P
P(Presença)
F(Falta)
terça-feira, 23 de junho de 2009
Equipe....
Nosso trabalho foi dividido em três partes o blog, a peça teatral e as questões no quadro , minha equipe é composta por 15 pessoas :
Ana Técia
Nayane Sabino
Niele
Keyliane
Carvalho
Maria Luíza
Nilzilândia
Janiele
Janily
Dayane Portela
Dayane Monteiro
Edvânia
Kervelly
Rafael Araújo
Leydiane
quinta-feira, 28 de maio de 2009
Conceitos básicos de circunferência
O estudo da circunferência na trigonometria é de grande importância, pois ela proporciona a construção de um ciclo trigonométrico que facilita o trabalhado no estudo trigonométrico de ângulos que não são agudos, tornando o estudo da trigonometria mais completo.
O que é circunferência?
Imagine um ponto P qualquer, todos os pontos distintos e eqüidistantes a ele irá formar uma circunferência.
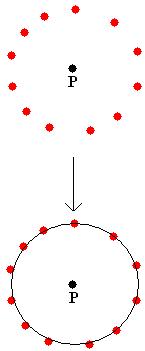
Esse ponto P é considerado o centro da circunferência, pois todos os pontos que pertencem à circunferência estão na mesma distância do ponto P. Essa distância é chamada de raio da circunferência.
Arco de circunferência
Arco de uma circunferência é, de uma maneira mais formal, uma parte do comprimento de uma circunferência que é delimitado por dois pontos quaisquer que pertence à circunferência. Veja como é feita essa representação:
Considere uma circunferência de centro P e com A e B pontos pertencentes a essa circunferência:
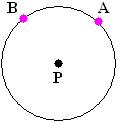
As partes delimitadas da circunferência pelos pontos A e B são chamadas de arcos da circunferência. Esses arcos possuem medidas de comprimentos.
Dois pontos quaisquer pertencentes a uma circunferência formam dois arcos.

O arco de medida x é representado por e
e 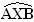 .
.
O arco de medida y é representado por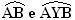 .
.
Sabemos que um arco de circunferência é delimitado por dois pontos que pertencem à circunferência, se esses pontos forem iguais, ou seja, estiverem localizados no mesmo lugar na circunferência, o arco será nulo ou de uma volta completa.
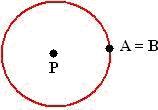
Ângulo central
Todo ângulo é formado pela abertura de dois segmentos de reta. O ângulo central é formado por duas retas que partem do centro e vão de encontro com os dois pontos da circunferência. A abertura dessas duas retas determina a medida do ângulo.
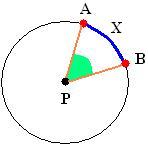
O arco subtende o ângulo central
subtende o ângulo central  , formado pelos segmentos de reta AP e PB,
, formado pelos segmentos de reta AP e PB,
ou seja:
med ( ) = med (
) = med ( 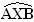 ).
).
O que é circunferência?
Imagine um ponto P qualquer, todos os pontos distintos e eqüidistantes a ele irá formar uma circunferência.

Esse ponto P é considerado o centro da circunferência, pois todos os pontos que pertencem à circunferência estão na mesma distância do ponto P. Essa distância é chamada de raio da circunferência.
Arco de circunferência
Arco de uma circunferência é, de uma maneira mais formal, uma parte do comprimento de uma circunferência que é delimitado por dois pontos quaisquer que pertence à circunferência. Veja como é feita essa representação:
Considere uma circunferência de centro P e com A e B pontos pertencentes a essa circunferência:

As partes delimitadas da circunferência pelos pontos A e B são chamadas de arcos da circunferência. Esses arcos possuem medidas de comprimentos.
Dois pontos quaisquer pertencentes a uma circunferência formam dois arcos.

O arco de medida x é representado por
O arco de medida y é representado por
Sabemos que um arco de circunferência é delimitado por dois pontos que pertencem à circunferência, se esses pontos forem iguais, ou seja, estiverem localizados no mesmo lugar na circunferência, o arco será nulo ou de uma volta completa.

Ângulo central
Todo ângulo é formado pela abertura de dois segmentos de reta. O ângulo central é formado por duas retas que partem do centro e vão de encontro com os dois pontos da circunferência. A abertura dessas duas retas determina a medida do ângulo.
O arco
ou seja:
med (
terça-feira, 26 de maio de 2009
Sabemos que o ângulo reto mede 90º e que o ângulo raso mede 180º. Mas por que motivo os valores são 90 e 180?

No ano de 4000 a.C., os egípcios e árabes tentavam elaborar um calendário. Nessa época, se acreditava que o Sol levava 360 dias para completar a órbita de uma volta em torno da Terra. Assim, a cada dia o Sol percorria um pouquinho dessa órbita, ou seja, um arco de circunferência de sua órbita. Esse ângulo passou a ser uma unidade de medida e foi chamado de grau.
Então, para os antigos egípcios e árabes, o grau era a medida do arco que o Sol percorria em torno da Terra durante um dia. Porém, hoje sabemos que é a Terra que gira em torno do Sol, mas se manteve a tradição e se convencionou dizer que o arco de circunferência mede um grau quando corresponde a 1/360 dessa circunferência.
Sábio grego mediu a circunferência da Terra com grande precisão em 300 a.C.?

A maior façanha científica da História pertence ao sábio grego Eratóstenes (300 anos a.C.). Mediu a circunferência da Terra com grande precisão, apenas comparando a diferença das sombras projetadas pelos objetos, no mesmo momento, em duas cidades distintas - Alexandria e Siene (hoje Assuã). Obteve 43.200 quilômetros - apenas 9,27% a mais do que os 40.075 quilômetros medidos com os instrumentos modernos.
Por que a circunferência tem 360 graus?
Não se sabe ao certo o motivo pelo qual se estabeleceu que a circunferência seria dividida em 360 graus. Existem pelo menos duas possibilidades. Na primeira delas, o número teria sido estabelecido por uma civilização que acreditava ser a terra o centro do universo e cujo calendário teria 360 dias. De acordo com a suposta civilização, o Sol caminharia, então, um grau por dia, totalizando os 360 graus da circunferência. Outra possibilidade é a de que os babilónios usavam 60 como base para seus cálculos. Por esse motivo, os gregos teriam dividido o raio do círculo em 60 partes. Como já seria conhecido que o comprimento da circunferência equivaleria a 2.Pi.r - duas vezes Pi vezes o raio - e que Pi valia aproximadamente 3, então teria se estabelecido que a circunferência teria 360 graus (2 x 3 x 60 = 360).
Assinar:
Comentários (Atom)